сколько будет риса на шахматной доске
Притча про шахматы
Сегодня я напишу любимую мною притчу, я знаю что многие из вас ее знают, но она послужит лишь поводом для размышлений в комментариях. А может ктото откроет для себя коечто новое если ее еще не слышал.
Притча про шахматы
Притча про шахматы
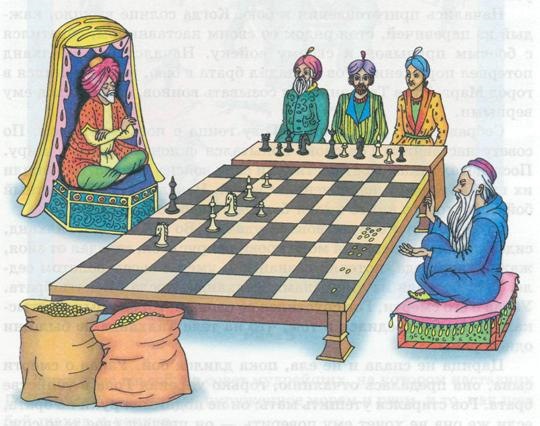
Шахматная игра была придумана в Индии, и когда индийский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что игра изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель — его звали Сета — явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
— Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал,— сказал царь.
— Я достаточно богат, чтобы исполнить самое смелое твое пожелание,— продолжал царь.— Назови награду, которая тебя удовлетворит, и ты получишь ее.
— Не робей,— ободрил его царь.— Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его!
— Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.
Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.
— Повелитель,— сказал Сета,— прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
— Простое пшеничное зерно? — изумился царь.
— Да, повелитель. За вторую клетку прикажи выдать два зерна, за третью — четыре, за четвертую — 8, за пятую— 16, за шестую — 32…
— Довольно! — с раздражением прервал его царь.— Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай! Слуги мои вынесут тебе мешок с пшеницей.
Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.
— Повелитель,— был ответ,— приказание твое, исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился — он не привык, чтобы повеления его исполнялись так медлительно.
Вечером, отходя ко сну, царь Шерам еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
— Повелитель,— ответили ему,— математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.
— Почему медлят с этим делом?! — гневно воскликнул царь.— Завтра, прежде чем я проснусь, всё до последнего зерна должно быть выдано Сете. Я дважды не приказываю!
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.
— Прежде чем скажешь о твоем деле,— объявил Шерам.— я желаю услышать, выдана ли наконец Сете та ничтожная награда, которую он себе назначил.
— Ради этого я и осмелился явиться перед тобой в столь ранний’ час,— ответил старик.— Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…
— Как бы велико оно ни было,— надменно перебил царь,— житницы мои не оскудеют! Награда обещана и должна быть выдана…
— Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыри. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.
С изумлением внимал царь словам старца.
— Назови же мне это чудовищное число,—сказал он в раздумье.
— Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три миллиарда семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!
Задача о зёрнах на шахматной доске.
Когда создатель шахмат, древнеиндийский мудрец и математик Сисса бен Дахир, показал своё изобретение Правителю страны, тому так понравилась игра, что он позволил изобретателю право самому выбрать награду. Мудрец попросил у Повелителя за первую клетку шахматной доски заплатить ему одно зерно пшеницы (по другой версии — риса), за второе — два, за третье — четыре и т. д., удваивая количество зёрен на каждой следующей клетке. Правитель, не разбиравшийся в математике, быстро согласился, даже несколько обидевшись на столь невысокую оценку изобретения, и приказал казначею подсчитать и выдать изобретателю нужное количество зерна. Однако, когда неделю спустя казначей всё ещё не смог подсчитать, сколько нужно зёрен, правитель спросил, в чём причина такой задержки. Казначей показал ему расчёты и сказал, что расплатиться невозможно, поскольку колличество зерна превышает весь урожай пшеницы, собранный за всю историю человечества.
На всей доске будет 2 в 64 степени − 1 или 18 446 744 073 709 551 616 зёрен, их общая масса составит 461 168 602 000 тонн. Для того, чтобы вместить такое колличество зерна потребуется амбар с размерами 10х10х15 км.
Правитель, чтобы взять реванш над пытавшимся его обхитрить изобретателем, велел последнему пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
 netumenya
netumenya
Есть Только Настоящее.
Сколько будет зёрен на шахматной доске, если класть на каждую следующую клетку доски вдвое больше зёрен, чем на предыдущую, начиная с одного?
18 446 744 073 709 551 615 зёрен, их общая масса составит 461 168 602 000 тонн.
Звучит это число так: Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать.
Когда создатель шахмат показал своё изобретение правителю страны, тому так понравилась игра, что он позволил изобретателю право самому выбрать награду. Мудрец попросил у короля за первую клетку шахматной доски заплатить ему одно зерно пшеницы (по другой версии — риса), за второе — два, за третье — четыре и т. д., удваивая количество зёрен на каждой следующей клетке. Правитель, не разбиравшийся в математике, быстро согласился, даже несколько обидевшись на столь невысокую оценку изобретения, и приказал казначею подсчитать и выдать изобретателю нужное количество зерна. Однако, когда неделю спустя казначей всё ещё не смог подсчитать, сколько нужно зёрен, правитель спросил, в чём причина такой задержки. Казначей показал ему расчёты и сказал, что расплатиться невозможно. Правитель, чтобы взять реванш над пытавшимся его обхитрить изобретателем, велел последнему пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Притча про шахматы
Шахматная игра была придумана в Индии, и когда индийский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что игра изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель — его звали Сета — явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
— Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал,— сказал царь.
— Я достаточно богат, чтобы исполнить самое смелое твое пожелание,— продолжал царь.— Назови награду, которая тебя удовлетворит, и ты получишь ее.
— Не робей,— ободрил его царь.— Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его!
— Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.
Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.
— Повелитель,— сказал Сета,— прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
— Простое пшеничное зерно? — изумился царь.
— Да, повелитель. За вторую клетку прикажи выдать два зерна, за третью — четыре, за четвертую — 8, за пятую— 16, за шестую — 32…
— Довольно! — с раздражением прервал его царь.— Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай! Слуги мои вынесут тебе мешок с пшеницей.
Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.
— Повелитель,— был ответ,— приказание твое, исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился — он не привык, чтобы повеления его исполнялись так медлительно.
Вечером, отходя ко сну, царь Шерам еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
— Повелитель,— ответили ему,— математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.
— Почему медлят с этим делом?! — гневно воскликнул царь.— Завтра, прежде чем я проснусь, всё до последнего зерна должно быть выдано Сете. Я дважды не приказываю!
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.
— Прежде чем скажешь о твоем деле,— объявил Шерам.— я желаю услышать, выдана ли наконец Сете та ничтожная награда, которую он себе назначил.
— Ради этого я и осмелился явиться перед тобой в столь ранний’ час,— ответил старик.— Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…
— Как бы велико оно ни было,— надменно перебил царь,— житницы мои не оскудеют! Награда обещана и должна быть выдана…
— Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыри. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.
С изумлением внимал царь словам старца.
— Назови же мне это чудовищное число,—сказал он в раздумье.
— Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три миллиарда семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!
Задача о зёрнах на шахматной доске — математическая задача, в которой вычисляется, сколько будет зёрен на шахматной доске, если класть на каждую следующую клетку доски вдвое больше зёрен, чем на предыдущую, начиная с одного.
Как правило, задача решается для стандартной 64-клеточной доски; при удвоении количества зёрен на каждой последующей клетке сумма зёрен на всех 64 клетках определяется выражением:
что составляет 18 446 744 073 709 551 615.
Задача и её вариации используются для демонстрации высокой скорости роста экспоненциальных последовательностей.
/привет/мир/etc
Непериодические заметки о программировании
воскресенье, 30 марта 2014 г.
Шахматная доска с рисом
Что общего между этой легендой и двоичной системой счисления?
Поскольку ни одна клетка не должна быть пропущена, то в каждом из 64-х разрядов двоичного числа стоит 1, и это максимальное число, которое можно записать в 64 двоичных разрядах:
Заглянув в Википедию, я смог произнести это число: 18 квинтиллионов 446 квадриллионов 744 триллиона 73 миллиарда 709 миллионов 551 тысяча 615.
К слову, это число больше, чем число секунд, прошедших с момента Большого Взрыва:
13800000000 * 365.25 * 24 * 60 * 60 = 435 494 880 000 000 000
Итак, это максимальное целое число, которое можно представить в 64-хразрядном кодовом слове. Большинство изготовляемых сегодня персональных компьютеров оперируют именно 64-разрядными двоичными словами.
Но вернемся к рисовым зернам на шахматной доске.
Если присмотреться к тому, как возрастает количество зерен на доске, то мы увидим, что заполнение каждой следующей клетки удваивает общее количество зерен на доске! Точнее, удваивает и добавляет еще одно зернышко. Вот результаты заполнения нескольких клеток подряд:
| N клетки | Кол-во зерен в клетке | Всего зерен на доске |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 1 + 2 = 3 |
| 3 | 4 | 3 + 4 = 7 |
| 4 | 8 | 7 + 8 = 15 |
| 5 | 16 | 15 + 16 = 31 |
| 6 | 32 | 31 + 32 = 63 |
Так, после заполнения 5 клеток на доске 31 зерно, а после выкладывания еще 32 зерен на 6-ю клетку общее количество зерен становится 63. То есть, на каждую последующую клетку выкладывается зерен на одно больше, чем общее количество зерен на всех предыдущих клетках!
Этим эффектом мы обязаны свойствам позиционной двоичной системы счисления, которую имитирует шахматная доска с рисом. Заполняя очередную клетку, мы добавляем к сумме рисовых зерен число, равное очередной степени двойки. Это все равно, что дописывать к двоичному числу единицу в очередной разряд слева, причем все разряды числа уже содержат единицы:
| N клетки | Кол-во зерен в клетке | Всего зерен на доске | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 = 12| 1 = 12 | 2 | 2 = 102 | 3 = 112 | 3 | 4 = 1002 | 7 = 1112 | 4 | 8 = 10002 | 15 = 11112 | 5 | 16 = 100002 | 31 = 111112 | 6 | 32 = 1000002 | 63 = 1111112 | |
Чтобы эффект ‘удвоение плюс один’ работал, нужно, чтобы разряды числа, к которому слева дописывается единица, имели максимально возможные в данной системе счисления значения. Тогда дописывание к числу единицы слева равносильно прибавлению к нему числа, которое на 1 больше первоначального.
Обратим внимание, что сумма весов единичных разрядов двоичного числа равна самому этому двоичному числу. Достаточно посмотреть на последний столбец вышеприведенной таблички.
Справедливость последнего наблюдения следует из известного нам представления k-разрядного числа в виде многчлена:
И еще одно наблюдение над шахматной доской с рисом.
Вес каждого следующего разряда (каждый следующий член геометрической прогрессии) равен весу предыдущего разряда (предыдущему члену), умноженному на основание системы счисления (знаменатель геометрической прогрессии):
В статье Считаем до 1000. на пальцах на основе наблюдений мы научились определять количество разных значений, которые можно представить в n разрядах числа по формуле:
Но количество разных значений, которые можно представить в n разрядах числа, равно весу n+1-го разряда. Так, в 2 разрядах десятичного числа можно представить сто разных значений, от 00 до 99:
И вес третьего справа разряда десятичного числа также равен 100. Изменим формулу так, чтобы она давала нам вес n-го разряда:
Это, по сути, формула для получения n-го члена геометрической прогрессии, где первый элемент прогрессии (вес младшего разряда) равен 1. Полностью формула для получения n-ного члена геометрической прогрессии выглядит так:
На этом оставляю шахматную доску с рисом мудрецу и правителю. Надеюсь, что требование мудреца было шуткой с его стороны, а правитель обладал достаточным тактом, чтобы мирно разрешить ситуацию.

 netumenya
netumenya