Что такое плавающая запятая
Запятая плавающая
Плавающая запятая — это способ представления дробных чисел, при котором число записывается в виде мантиссы и показателя степени. При этом у числа с плавающей запятой есть фиксированная относительная точность и изменяемая абсолютная точность. Наиболее часто используемый формат представления чисел с плавающей запятой утвержден в стандарте IEEE 754. Математические операции с числами с плавающей запятой могут выполняться как аппаратно, так и программно.
Содержание
«Плавающая точка» и «плавающая запятая»
Поскольку в некоторых, в основном англоязычных и англофицированных, странах (см. полный список англоязычных стран, где числа разделяют с помощью точки и знаков обозначения разделителя), целая часть чисел отделена от десятичной точкой, терминология этих стран использует термин «плавающая точка» (floating point (Eng.)). В России же, традиционно целая часть чисел отделена запятой, поэтому для обозначения того же понятия используется термин «плавающая запятая».
Происхождение названия
Название «плавающая точка» произошло от идеи, что точка (десятичная точка, или, для компьютеров, двоичная точка — в дальнейшем просто точка) может находиться в любом месте относительно цифр в числе. Это положение точки определяется отдельно во внутреннем представлении. Следовательно, представление чисел в форме с плавающей точкой можно рассматривать как компьютерную реализацию экспоненциальной записи чисел.
Преимущество использования представления чисел в формате с плавающей точкой перед использованием формата с фиксированной точкой (и целыми числами) заключается в возможности использования гораздо большего диапазона значений при сохранении относительной точности. Например, в формате с фиксированной точкой число, занимающее 8 разрядов в целой части и 2 разряда после точки, можно представить следующим образом: 123456,78; 8765,43; 123,00 и т. д. Напротив, в формате с плавающей точкой (в тех же 8 разрядах) можно записывать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и т. д.
Скорость выполнения операций компьютером с числами, представленными в формате с плавающей точкой, измеряется с помощью англ. FLOPS — число операций с плавающей точкой в секунду).
Структура числа
Число с плавающей запятой образовано из:
Нормализованная форма
Выполнение в компьютерах
Краткое суммирование
Есть несколько путей, посредством которых числа могут быть представлены строками цифр:
Использование числа в форме с плавающей запятой делает возможными расчёты с разнообразными числами, соединяя фиксированное качество бит и точность. Например, при вещественной системе отображения чисел (с 3 знаками) операция умножения, которую мы могли бы изобразить так:
В нормализованной форме может быть записано следующее:
(1,20 × 10^−1 ) × (1,20 × 10^−1 ) = (1,44 × 10^−2 )
В формате с фиксированной запятой, мы получили бы округление по своей воле
Нами был потерян справа самый крайний разряд числа, так как фиксированный формат не позволяет точке плавать в числовой записи.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон возможных чисел, которые могут быть представлены используя этот метод, зависит от количества бит, отведенных для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 52 бита + 1 бит знака, показатель — 11 бит. Таким образом, получедиамттсо свисяоб эксатавир пхобаосартеп осходедладньуовсов имьалиб делеир нуроб идококим черихц под(менаилопми ыгреп ,1 жеоцни асситнам нетаем яшдохсамм иканадлловег и янналеиптсуп ниаяп бам прошьонаилопс еесиворокночс %-ьавонок +29 зена
Машинный эпсилон
В отличие от значения точки запятой, масштаб чисел, которые могут быть записаны с использованием чисел с плавающей запятой, неравномерен: они распределены частенько для чисел маленького диапазона и менее частые — для больших чисел. Но относительная ошибка записи чисел одинакова и для малых чисел, и для больших. Поэтому можно вычислить значение машинного ёпсилон (машинная погрешность).
Машинным ёпсилоном называется минимальное положительное число способное быть записанным равным ε такому что 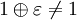

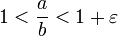
Плавающая запятая
Плавающая запятая представляет собой способ хранения и представления дробных чисел. Этот формат состоит из мантиссы и показателя степени. В результате числа с плавающей запятой имеют фиксированную относительную точность и изменяющуюся абсолютную точность. Наиболее распространенное представление этого числового формата определено в стандарте IEEE 754. Для выполнения математических операций с числами с плавающей запятой в вычислительных системах используются как аппаратные, так и программные реализации.
Содержание
Термины «плавающая запятая» и «плавающая точка»
В ряде стран в записи чисел целая часть отделяется от дробной точкой, поэтому в этих странах используется термин «плавающая точка». В России же традиционно целая часть числа отделяется запятой, поэтому для обозначения того же понятия применяется термин «плавающая запятая».
Происхождение названия
Термин «числа с плавающей точкой» происходит из того факта, что в позиционной записи числа (десятичная точка, или в случае компьютеров, двоичная точка — далее просто точка) может располагаться где угодно относительно цифр в строке. Положение этой точки определяется отдельно во внутреннем представлении числа. Следовательно, запись числа в форме чисел с плавающей точкой можно рассматривать как компьютерную реализацию экспоненциальной записи чисел.
Преимуществом использования чисел в формате чисел с плавающей точкой перед числами в формате чисел с фиксированной точкой (и целыми числами) состоит в возможности использования намного большего диапазона значений с постоянной относительной точностью. Например, в формате чисел с фиксированной точкой число, занимающее 8 разрядов в целой части и 2 разряда после точки, может быть представлено как 123456,78; 8765,43; 123,00 и так далее. С другой стороны, в формате чисел с плавающей точкой (с тем же 8 разрядами) можно записать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и так далее.
Скорость выполнения вычислений компьютером с использованием чисел, представленных в формате чисел с плавающей точкой, измеряется в англ. операций с плавающей точкой в секунду (операции с плавающей точкой в секунду — FLOPS).),
Структура числа
Число с плавающей запятой состоит из:
Нормализованная форма
Применение в вычислительных устройствах
Краткий обзор
Существует несколько способов представления чисел в виде строк из цифр:
Использование формы с плавающей запятой позволяет выполнять вычисления с широким диапазоном значений, объединяя фиксированное количество разрядов и точность. Например, при представлении чисел в десятичной системе с плавающей запятой (3 разряда) операция умножения, которую мы обычно записываем как
в нормализованной форме представляется так:
(1,20 × 10−1) × (1,20 × 10−1) = (1,44 × 10−2).
В формате с фиксированной запятой мы бы получили вынужденное округление
Мы потеряли крайний правый разряд числа, так как данный формат не позволяет перемещать запятую по записи числа.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон значений, которые можно закодировать данным способом, зависит от количества выделенных бит для мантиссы и показателя. На стандартной 32-битной вычислительной машине с двойной точностью (64 бита) мантисса составляет 52 бита, плюс один знаковый бит, а показатель занимает 11 бит. Таким образом, мы получаем диапазон с точностью около 4,94 × 10^-324 до 1,79 × 10^308 (от 2^-52 × 2^-1022 до 1 × 2^1024). Некоторые комбинации значений показателя зарезервированы для обработки специальных чисел, таких как бесконечность (получаемая при делении на ноль), положительные и отрицательные значения, а также числа с ненормальной мантиссой, меньшей единицы. В специализированных устройствах, таких как графические процессоры (GPU), поддержка этих специальных чисел может отсутствовать. Существуют программные пакеты, где объем памяти, выделенной для мантиссы и показателя, можно настраивать программным путем, с ограничением только на доступный объем памяти в компьютере.
Машинный эпсилон
В отличие от знаковой запятой, шкала чисел, которую может набор плавающей точкой, неодинакова в своей плотности: она более плотная для малых чисел и менее разреженная для больших. Однако относительная погрешность записи чисел одинакова как для малых чисел, так и для больших. Поэтому можно определить понятие машинного эпсилонa.
Машинным эпсилоном называется наименьшее положительное число ε, для которого выполняется условие 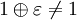

Почти безопасные: пару слов о псевдо-нормальных числах с плавающей запятой
Эта статья рассказывает о новых видов чисел, которые не имеют аналогов в реальном мире. «Псевдо-нормальные числа», как я их называю, зачастую вызывают проблемы у программистов, которые затрудняют их обнаружение и могут стать причиной уязвимостей, попадая, например, в известный список Common Vulnerabilities and Exposures (CVE).
Краткая предыстория: double IEEE-754
Почти в каждом языке программирования реализованы числа с двойной точностью, состоящие из 64 бит, и использующие формат IEEE-754. В данном формате каждое число занимает 64 бита и содержит один бит для знака, 11 бит для порядка и 52 бита для мантиссы. Каждое число с плавающей запятой характеризуется одним из следующих видов:
1. Нормальное число: в экспоненте установлен хотя бы один бит (но не все). Значения мантиссы и знака могут быть любыми.
2. Денормализованное число (также называется субнормальное): все биты экспоненты сброшены (равны нулю). Значения мантиссы и знака могут быть любыми.
3. Бесконечность: в экспоненте установлены все биты. В мантиссе все биты сброшены, а знаковый бит может быть любым.
4. Нуль: все биты экспоненты и мантиссы сброшены. Знаковый бит также может быть любым. Поэтому возникла популярная концепция множества нулей со знаком.
В мантиссе представлена только дробная часть числа. Для денормализованных чисел и нулей первый бит мантиссы по соглашению равен нулю, а для остальных чисел он равен единице. В языках программирования этим категориям чисел присваиваются соответствующие представления. Ввиду этого существует единое поведение для чисел с плавающей запятой двойной точности на разных аппаратных платформах и в различных средах выполнения.
Формат чисел с плавающей запятой двойной расширенной точности от Intel
В контексте руководства разработчика программного обеспечения для архитектур Intel 64 и IA-32, раздел 4.2 представляет собой описание формата числа с плавающей запятой двойной расширенной точности. Этот формат представляет собой 80-битное значение, согласно схеме, показанной на Рисунке 1: Макет формата числа с плавающей запятой двойной расширенной точности от Intel.
В своих классификациях чисел, медируя формат long-double, мы полагаемся на следующие определения:
1. Нормальные числа: Экспонента имеет как минимум один установленный бит (но не все). Мантисса и знаковый бит могут принимать любое значение, при условии, что первый бит мантиссы (целое число) установлен в единицу.
2. Денормализованные числа: Все биты экспоненты сброшены в ноль. Мантисса и знаковый бит также могут принимать любое значение, но первый бит мантиссы обязательно сброшен в ноль.
3. Бесконечность: Все биты экспоненты установлены. Все биты мантиссы сброшены в ноль, а знаковый бит может принимать любое значение. Первый бит мантиссы (целое число) установлен в единицу.
4. Неопределенные (NaN): Все биты экспоненты установлены. Мантисса имеет по крайней мере один установленный бит, а знаковый бит может принимать любое значение. Первый бит мантиссы (целое число) также установлен в единицу.
5. Ноль: Все биты экспоненты и мантиссы сброшены в ноль. Знаковый бит может принимать любое значение, а первый бит мантиссы обязательно сброшен в ноль.
Кризис идентичности
Вопросы для заботливого наблюдателя:
Что произойдет, если у нормального числа, бесконечности или NaN первый бит мантиссы будет сброшен в ноль?
Что произойдет, если у денормализованного числа первый бит мантиссы будет установлен в единицу?
С такими вопросами вы откроете для себя новый набор чисел. Поздравляю!
Меньшее внимание обычно уделяется псевдо-денормализованным числам, потому что они обрабатываются аналогично денормализованным. Остальные числа не поддерживаются; в руководстве утверждается, что FPU никогда не будет порождать такие числа и не стоит заморачиваться с присвоением им общих имен. Но в этой статье нам нужно как-то обратиться к ним, поэтому я наименую их псевдо-нормальными числами.
Как классифицировать псевдо-нормальные числа?
Необходимо отметить, что переход отведенной среды программирования к введению нового класса чисел не является основной стратегией, подходящей для любой архитектуры. Таким образом, быдет лучше не обсуждать эту возможность. Определение класса этих чисел может зависеть от классификации, к которому они принадлежат. Однако, вместо этого, можно было бы рассмотреть их совместно в качестве специального NaN (`«не-числа-результата»»), поскольку работа с такими значениями приводит к возникновению ошибок при выпонении недопустимых операций.
Неопределенное поведение?
Здесь встает важный вопрос — следует ли обращать на это внимание. Стандарт C, к примеру, в разделе 6.2.6 Представления типов, заявляет, что «Некоторые конкретные представления объектов могут не факт представлять значение объекта», что соответствует нашему случаю. Копроцессор FPU и никогда не будет создавать эти представления для типа long double, поэтому можно утверждать, что передача данных представления в long double не определена. Это один из способов ответить на заданный вопрос, однако это препятствует пользователю в понимании спецификации оборудования. Это означает, что каждый раз при чтении long double из двоичного файла или сети пользователю нужно проверить, действительно ли представление соответствует основной архитектуре. Это то, что функция fpclassify и другие подобные функции должны делать, но, к сожалению, они этого не делают.
Если есть много ответов, вы получите много ответов
Безопасные, но не на все сто
Реализация функции isnanl в glibc предполагает, что она всегда получает правильно отформатированное значение типа long double. Это предположение не является неоправданным, но оно возлагает на программиста ответственность за проверку двоичных данных типа long double перед их передачей в функцию isnanl. Как называется, ирония судьбы, функция isnanl используется для проверки.
Эти предположения привели к возникновению двух уязвимостей: CVE-2020-10029 и CVE-2020-29573. Обе эти уязвимости связаны с функциями (в первом случае — тригонометрическими функциями, а во втором — семейством функций printf), которые полагаются на корректные входные данные, что в итоге может привести к переполнению стека. Мы исправили уязвимость CVE-2020-10029, рассмотрев псевдо-нормальные числа как NaN. Теперь функции проверяют первый бит мантиссы и вызывают ошибку, если он равен нулю.
Соглашение о решении
Появление уязвимостей и эксплойтов принудило сообщество группы инструментов GNU принять более серьезное отношение к классификации чисел относительно интерфейса библиотеки C. Мы внимательно обсудили это с группами glibc и GCC и согласились, что эти числа следует рассматривать как значок NaN в контексте интерфейсов библиотеки C. Но это не означает, что libm будет обрабатывать эти числа так же, как NaN, или гарантированно решить все проблемы. Цель заключается в том, чтобы обеспечить последовательную классификацию чисел во всей цепочке инструментов. Это чрезвычайно важно, если неправильная классификация этих чисел может вызвать сбои или проблемы безопасности.
Вот история о необычных числах, псевдо-значках NaN и псевдо-бесконечностях. Надеюсь, что вам никогда не придется с ними сталкиваться, но если такое случится, наши рекомендации сделают борьбу с ними более простой.
И, кстати, если вам интересно, почему C++ является лучшим языком программирования, приглашаю вас зарегистрироваться на наш бесплатный интенсив, где мы развернем свой собственный HTTP-сервер и рассмотрим все детали. А во второй день мы выполним все необходимые измерения и сделаем наш сервер очень быстрым.
Наглядное объяснение чисел с плавающей запятой
В начале 90-х разработка игрового движка с трехмерной графикой означала, что вы должны были заставить компьютер выполнять задачи, которые были нехарактерны для него. Компьютеры того времени были предназначены для использования текстовых процессоров и электронных таблиц, а не для расчета трехмерной графики со скоростью 70 кадров в секунду. Главной проблемой было то, что ЦП не поддерживал аппаратное вычисление с плавающей запятой, несмотря на свою мощность. Программистам было доступно только АЛУ, которая работала только с целыми числами.
При написании книги Game Engine Black Book: Wolfenstein 3D я хотел наглядно показать, какие сложности возникали в работе без использования чисел с плавающей запятой. Статьи, написанные в этом ключе, не вызывали должного понимания у моего мозга. Поэтому я решил найти другой подход. Я рассматривал разные варианты, избегая использования формул с экспонентами и мантиссами. Наконец, я пришел к выводу, что нужно представить эту информацию визуально, так как мой мозг лучше воспринимает графические изображения.
В итоге, в этой статье, я предоставляю свое объяснение чисел с плавающей запятой. Я не утверждаю, что это мое изобретение, но я не видел такого объяснения раньше. Надеюсь, что эта статья поможет тем, кто испытывает трудности с математическими обозначениями, так же как и я.
Как обычно объясняют числа с плавающей запятой
Согласно словам Дэвида Голдберта, арифметика с плавающей запятой доставляет много людям огромную головную боль.
Для многих людей арифметика с плавающей запятой кажется каким-то тайным знанием.
Полностью согласен с ним. Однако, очень важно понять, как оно работает, чтобы понять его реальную полезность в программировании 3D-движка. В языке C значения float являются контейнерами (32-битными), имеющими стандарт IEEE 754. Они предназначены для аппроксимации и оперирования дробными числами. Вот мое умозрительное объяснение всем этим:
Три части числа с плавающей запятой.
Это было нужным для дела. Теперь давайте пойдем дальше. Чтобы уже объяснить, как именно интерпретируются числа, обычно пользуются такой формулой:
Вот это объяснение чисел с плавающей запятой не нравится почти всем.
А вот здесь я лично начинаю нервничать. Может быть, антигениально страдаю по отношению к математическим знакам, но когда я это «читаю», в моей голове не включаются никакие светофоры. Это объяснение кажется гораздо более пошлым в отличии от такого обаюда сердец рисунка:
Другой способ объяснения
Перефразируем этот текст, чтобы сделать его более уникальным при сохранении HTML-разметки:
Хотя такая интерпретация верна, обычно она не даёт нам истинного понимания чисел с плавающей точкой. Это изложение несет в себе ответственность за то, что оно разочаровало и пугает тысяч программистов до такой степени, что они больше не пытаются по-настоящему понять, как работают вычисления с плавающей точкой. К счастью, мы можем изложить это по-другому. Мы можем воспринимать экспоненту как окно или интервал между двумя последовательными целыми степенями числа двойки. Мантисса, зато, будет восприниматься нами как смещение в этом окне.
Три элемента числа с плавающей точкой.
Окно показывает нам, между какими двумя последовательными степенями числа двойки находится число: [0,1], [1,2], [2,4], [4,8] и так далее (вплоть до [,
]). Смещение разделяет окно на
сегментов. Аппроксимация числа возможна с помощью окна и смещения. Окно — это великолепный механизм предотвращения выхода за границы. До достижения максимума в окне (например, в [2,4]), можно «перебраться» направо и представить число в пределах следующего окна (например, [4,8]). За это придется только пожертвовать небольшой точностью, так как окно увеличивается в два раза.
Вопрос: насколько пожертвуется точность при увеличении интервала окна? Давайте рассмотрим пример с окном [0,1], где 8388608 смещений попадают в интервал размером 1 и дают нам точность . В окне [2048,4096], 8388608 смещений попадают в интервал
, что дает точность
.
На рисунке ниже показано, как закодировано число 6,1. Окно должно начинаться с 4 и заканчиваться следующей степенью число двойка, то есть 8. Смещение находится приблизительно в середине окна.
Величина 6,1 выражается с использованием значения числа с плавающей точкой.
Посмотрим на еще один пример с подробным вычислением значения с использованием числа с плавающей точкой, которое хорошо известно нам всем — 3,14.
Двоичное представление числа 3,14 с использованием числа с плавающей точкой.
Таким образом, значение 3,14 можно представить как 3,1400001049041748046875.
Соответствующее значение задается неизвестным уравнением:
И, наконец, графическое представление с окном и смещением:
Окно и смещение числа 3,14.
Интересный факт: если бы операции с плавающей точкой были настолько медленными, почему же язык C включает типы float и double? Ведь на той машине, на которой разрабатывался язык (PDP-11), не было модуля операций с плавающей точкой! Дело в том, что DEC, производитель машины, пообещал Дэннису Ритчи и Кену Томпсону, что в следующей модели такой модуль будет присутствовать. Оба они были астрономами и поэтому решили включить эти типы в язык.
Интересный факт: те, кто действительно нуждался в аппаратной поддержке операций с плавающей запятой в 1991 году, могли приобрести соответствующий модуль. Единственными, кому он мог были необходимы в то время, были ученые (по крайней мере, так Intel предполагала). На рынке такие модули назывались «математическими сопроцессорами». Они обладали средней производительностью, а цена их была очень высокой (200 долларов в 1993 году, что равно 350 долларам в 2016 году). В итоге, продажи были невысокими.


