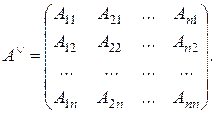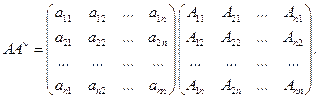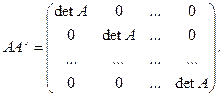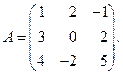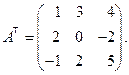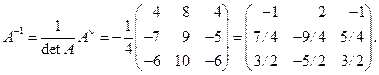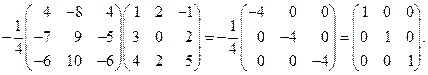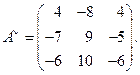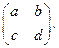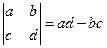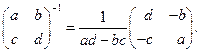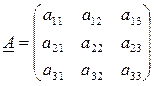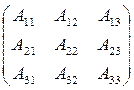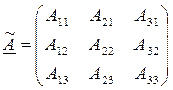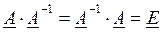Что такое присоединенная матрица

Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.

Невырожденная матрица – это матрица, определитель которой отличен от нуля. Следовательно, вырожденная матрица – это такая матрица, у которой определитель равен нулю.

Существует несколько способов для нахождения обратной матрицы, и мы рассмотрим два из них. На данной странице будет описан метод присоединенной матрицы, который является стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), включающий использование метода Гаусса или метода Гаусса-Жордана, будет рассмотрен во второй части.

Метод присоединённой (союзной) матрицы

Если решение аналитическое, то первый способ удобен только для небольших матриц: второго (пример №2), третьего (пример №3), четвертого (пример №4). Для матриц высших порядков используются другие методы, например, метод Гаусса, рассмотренный во второй части.

Итак, обратная матрица найдена:

$$A^<-1>=\left( \begin -8/103 & 7/103\\ 9/103 & 5/103 \end

ight).$$

Строим матрицу из алгебраических дополнений и транспонируем ее:

Для матрицы размерности четыре нахождение обратной матрицы с помощью алгебраических дополнений усложнено. Однако такие примеры встречаются на контрольных работах.

Например, для первой строки получим:

А далее продолжаем нахождение алгебраических дополнений:

Матрица из алгебраических дополнений:

Проверка, если нужно, может быть выполнена так же, как в предыдущих примерах.

Во второй части будет рассмотрен другой способ нахождения обратной матрицы, использующий преобразования метода Гаусса или метода Гаусса-Жордана.

Обнаружили ошибку, опечатку или неправильное отображение формулы? Оставьте сообщение на форуме (регистрация не требуется).

Источник

Обратная матрица

Перечень

Возможность в алгебре[правка]

[ math] xz = e, x [ / math] — левая взаимная

[ math] zy = e, y [ / math] — верный

回

Fact 2. Пусть [존재 z ^ ◼¼> /, / ¶25 < 부호83를 ​​>, \ 실험42 <보기95를 ​​>]

Критерий возможности матрицы [правка]

—

р지

Предположим [math] сниству‖ ca ]удs绣\ = o\уар>)y[`Фода5y+

g+i6µca/

Свойства обратной матрицы [ править ]

Методы нахождения обратной матрицы [ переработка ]

Метод Гаусса для вычисления обратной матрицы [ переработка ]

Пример [ переработка ]

Давайте найдем обратную матрицу для данной матрицы

Метод присоединенной матрицы [ переработка ]

Алгебраическое дополнение элемента [math]\ a_[/math] матрицы [math]\ A[/math] обозначается числом

[math]M_ = det\begin a_ <11>& a_ <12>& \cdots & a_ <1(j-1)>& a_ <1(j+1)>& \cdots & a_ <1n>\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_ <(i-1)1>& a_ <(i-1)2>& \cdots & a_ <(i-1)(j-1)>& a_ <(i-1)(j+1)>& \cdots & a_ <(i-1)n>\\ a_ <(i+1)1>& a_ <(i+1)2>& \cdots & a_ <(i+1)(j-1)>& a_ <(i+1)(j+1)>& \cdots & a_ <(i+1)n>\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ & a_ & \cdots & a_ \\ \end[/math]

Источник

Метод присоединенной матрицы

Опрeделение обратной матрицы

ОБРАТНЫЕ МАТРИЦЫ

ЛЕКЦИЯ 3

Обратная матрица Метод присоединенной матрицы. Матричные уравнения. Матричный способ решения систем линейных уравнений. Ранг матрицы. Метод окаймляющих миноров. Метод элементарных преобразований. Теорема о базисном миноре.

Матрица А –1 является обратной матрицей в отношении к матрице А, если выполняется равенство

Следуя данному определению, становится ясно, что обратные матрицы перестановочны. Другими словами, только квадратные матрицы могут иметь обратную. Тем не менее, не каждая квадратная матрица обладает обратной. Для матрицы А иметь обратную, необходимо и достаточно, чтобы ее определитель был ненулевым: detA¹0.

% Это подразумевает, что определитель равенство обратной матрицы и свойства определителей удовлетворяют требованию: det(A –1 A)=detA –1 detA=detE=1.Отсюда следует, что для существования обратной матрицы необходимо и достаточно условие detA¹0 или detA –1 ¹0. Вопрос о доказательстве достаточности этого условия несколько сложнее. Для ответа на него нужно описать процедуру построения такой матрицы. Поэтому мы рассмотрим этот вопрос позже (см. метод присоединенной матрицы).

Отметим, что если существует обратная матрица, то она является единственной. Иначе говоря, пусть существует матрица В, котора-satisfied АВ=ВА=Е, тогда можно записать:

Матрица, у которой определитель не равен нулю, называется с невырожденная матрица, или неособенная матрица; в противном случае, если добавить является коэффициентом, то он будет вырожденной матрицей, или сингулярная матрица. Единственное необходимое и достаточное условие существования обратной матрицы можно сформулировать следующим образом: Обратная матрица существует и является единственной, когда характеристическая матрица или исходная матрица невырождена.

У невырожденных матриц справедливы следующие свойства:

Матрица A Ú является присоединеным к матрице A, если она является ее транспонированной, используя в алгебра они хранятся equation elements, известны также эти условия.

Теорема 3.1. Обратная и присоединенная матрицы связаны соотношением

(3.2)

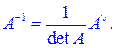
% Действительно, рассмотрим произведение матриц

При этом учтем, что сумма произведений элементов некоторой строки или столбца на их алгебраические дополнения равно определителю матрицы (см. теорему о разложении определителя по строке или столбцу).Дополнительно мы воспользуемся еще одним свойством определителей: сумма произведений алгебраических дополнений некоторой строки или столбца на соответствующие элементы другой строки или столбца равно нулю. Это связано с тем, что такая сумма эквивалентна определителю, у которого две одинаковые строки или столбца, и, следовательно, он будет равен нулю. Таким образом, перемножая рассматриваемые матрицы, получим

Отсюда следует справедливость приведенной теоремы. Более того, фактически мы указали алгоритм построения обратной матрицы при помощи присоединенной матрицы и тем самым доказали достаточное условие существования обратной матрицы. &

Общая схема нахождения обратной матрицы
(метод присоединенной матрицы):

1) Вычисляем определитель заданной матрицы, если он равен нулю, то обратной матрицы не существует.

2) Транспонируем заданную матрицу.

3) Вычисляем все алгебраические дополнения транспонированной матрицы.

4) Составляем присоединенную матрицу, т.е. вместо элементов транспонированной матрицы ставим их алгебраические дополнения.

5) Записываем обратную матрицу. Для этого каждый элемент присоединенной матрицы делим на определитель исходной матрицы.

Решение. 1) detA = –4.

2)

3) Ищем алгебраические дополнения транспонированной матрицы (не забывать учитывать знаки алгебраических дополнений!):

Перехождение к подматрице:

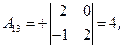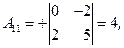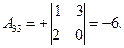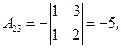Оказывается, после перепутаня столбцами:

Начном искать матрицу обратную марице H

Похожена на матрицу J:

Делегаем проверку: AA –1 = A –1 A = A:

Таким образом, обратный Mатirisру найден правильно. à

Пример 3.2. Маритиип СММатА{«п»}Матширумятво{«я»}ту ф cотпияту

Решение. Поскоф всех :

Показанное варо №2чна предотравокоуИсточник

Присоединенная матрица и алгоритм ее составления

Дата добавления: 2015-07-23; просмотров: 9564; Нарушение авторских прав

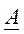
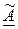
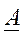
Для каждой квадратной матрицы , существует другая квадратная матрица с таким же порядком, которая называется присоединенной к матрице . При этом каждый элемент a_ij исходной матрицы заменяется его алгебраическим дополнением A_ij, а затем полученная матрица транспонируется.

Ex. Пусть дана исходная матрица порядка (3 ´ 3)

Чтобы составить присоединенную к данной матрице 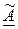, необходимо:

1. Найти для каждого элемента a_ij исходной матрицы его алгебраические дополнения A_ij и составить из них матрицу алгебраических дополнений.

2. Транспонировать полученную матрицу алгебраических дополнений.

12. Обратная матрица: условия ее существования
и алгоритм составления

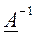
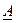
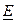
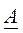
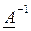
Def. Матрица называется обратной по отношению к квадратной матрице , если при перемножении этих матриц получается единичная матрица той же размерности, то есть:

Def. Матрица называется обратимой, если существует обратная матрица .

Ученёные доказали. Формула 1: Вышеуказанная матрица будет иметь обратную только если она является квадратной и невырожденной

Область научного доказательства существования матрицы Формула 2:

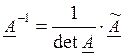то есть, процедура составления номера включает следующие основные шаги:

1. рассчитываем статистическую информацию исходной матрицы Выберите номер 1, и если это будет ноль, значит матрица Выберите номер 2, обратима и можно перейти к следующему шагу;

2. используя Формула 3 выбираем матрицу Выберите number3 в качестве приложения к исходной матрице Выберите номер 4;

3. Делите каждый элемент приложенной матрицы Выберите номер 5 на число Выберите number6, в итоге получится искаемая обратная матрица Выберите number7.

менее важные матрицы

Формула 41. При взаимно обратных матрицах выполняется помощниковая проверка действий умножения

2. Во время создания обратной матрицы получите оригинальную матрицу

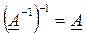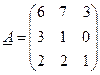Ажиотаж, заверазолжим матрицу что будет обратной для

1. Решением является матрица из определителя исходная матрица

2.Вычисляем алгебраические дополнения A_ij для каждого элемента a_ij оригинальной матрицы и формируем временную матрицу алгебраических дополнений

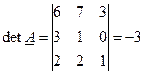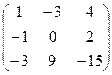
3.Путем транспонирования временной матрицы алгебраических дополнений, получаем результирующую матрицу

, присоединяем ее к оригинальной матрице

4.Делим каждый элемент результирующей матрицы на

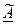
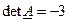
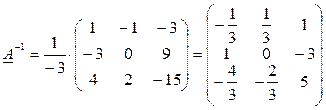Для проверки правильности вычислений умножаем оригинальную матрицу на полученную обратную, результат должен быть единичной матрицей

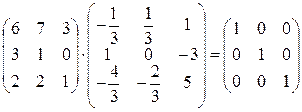Обратные матрицы широко используются для решения систем линейных уравнений в матричной форме, статистического анализа информационных массивов и решения других практических задач. Процесс формирования обратных матриц требует значительных объемов арифметических вычислений и обычно выполняется на компьютерах с использованием специализированных программ и процедур.

Если вы не нашли то, что искали, прибегните к помощи от Google!

Источник

Теорема. Опр. Матрица называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы

Определение:

Матрица A называется вырожденной, если ее определитель равен нулю (A = 0), и невырожденной, если ее определитель не равен нулю (A ≠ 0).

Пусть матрица A является невырожденной, то есть A ≠ 0. В таком случае, применяя правила перемножения матриц, теорему Лапласа и свойство 9 определителей, мы получаем следующее:

A × A^-1 = E,

где E — это единичная матрица.

Аналогично можно доказать, что A^-1 × A = E.

Свойства обратной матрицы:

Источник