Что такое предел в математике простыми словами
Что означает предел в математике
Изучаем особенности, связанные с применением слова «lim»
Все говорят о разности, а мы продолжаем анализировать сложные математические вопросы, чтобы они не выглядели такими сложными.
Что такое предел в математике
При обсуждении пределов matemathicsПо определению предел это последовательность участков в развитии событий:
Если говорить просто, то функция в математике — это стремление достичь определенного числа другим числом, но не достичь его полностью.
Например, когда переменная функции стремится к бесконечности, значение функции каждый раз больше предыдущего.
1, 2, 3, … 1000000000000003, 1000000000000004 и так далее в бесконечность.
С другой стороны, когда переменная функции стремится к нулю, значение функции постоянно уменьшается:
1, 0.1, 0.01, 0.001, … 0.00000000000000000000000001 — каждый раз число будет приближаться к нулю, но никогда его не достигать.
CAимвол стремления переменной к числу обозначается стрелкой: x→0, а слово «предел» обозначается символом lim:
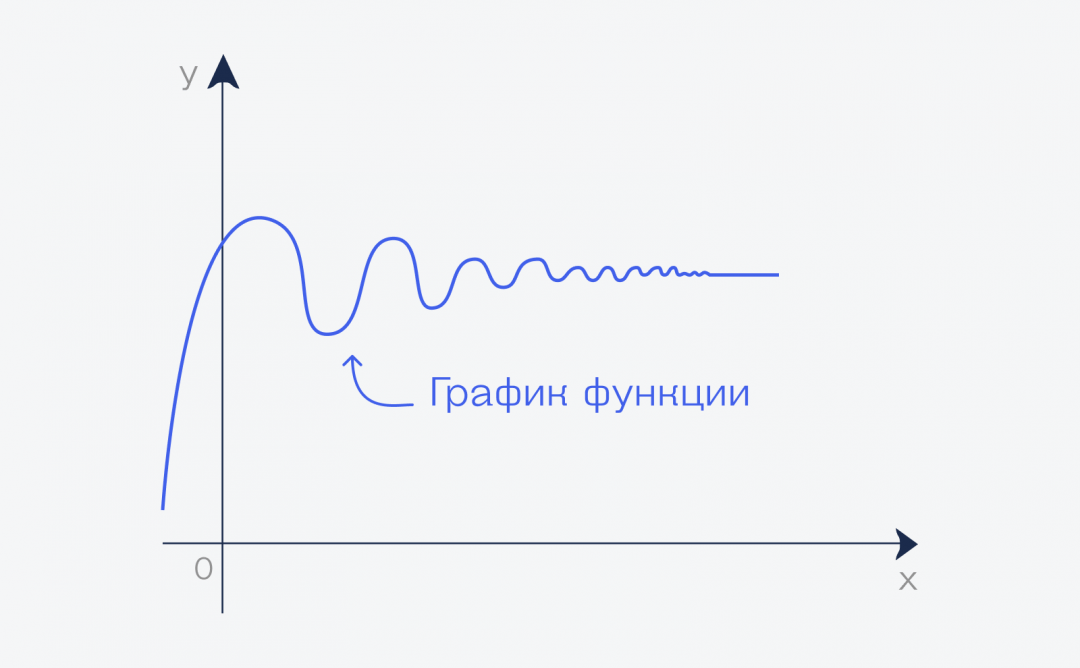
График и предел
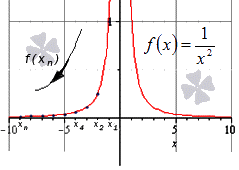
Если мы изобразим на графике данную функцию, мы можем увидеть, что начиная с определенного момента, она приближается к прямой линии вдоль оси. Хотя она никогда не станет полностью прямой, но продолжая рисовать график до бесконечности, она стремится к этому.
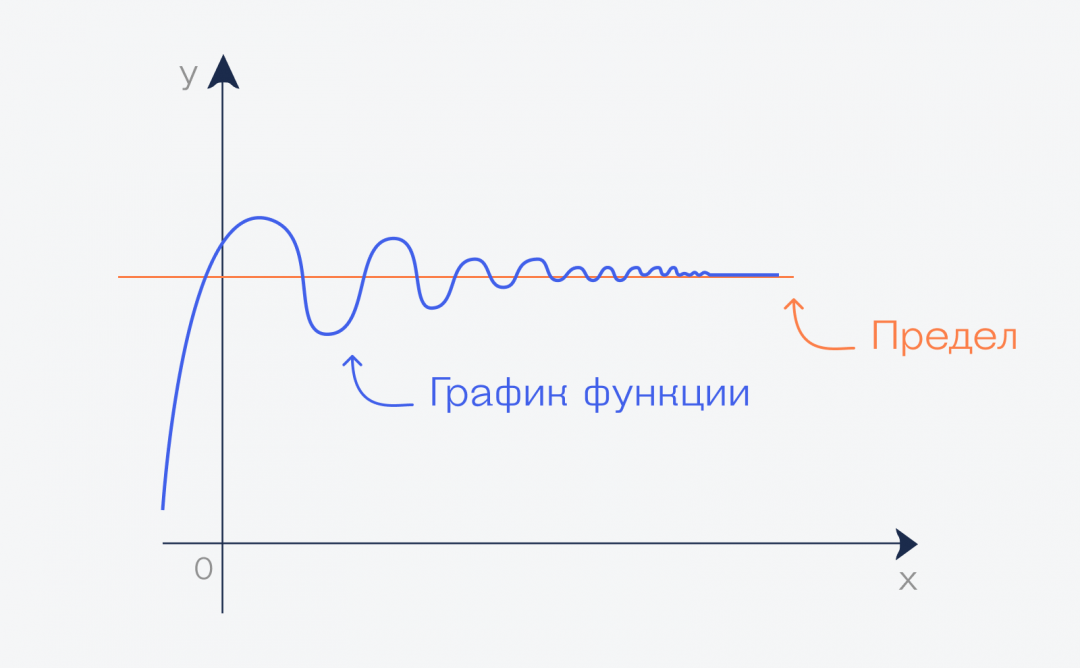
Бесконечный график означает, что значение переменной функции стремится к бесконечности. И значение линии на графике — это предел функции при переменной, стремящейся к бесконечности:
Пределы в жизни
Пределы в математике находят широкое применение при решении практических задач. Они помогают определить точку, после которой изменение результатов становится незаметным.
На примере строительства моста бригада монтажников должна определить максимально допустимую длину плиты перекрытия. Устанавливаются минимальные требования к прочности плиты в середине, а именно она должна выдерживать нагрузку в 50 тонн. Пределы помогают определить длину плиты, при которой ее прочность будет достаточной.
Пределы применяются астрономами для изучения законов Вселенной, физиками для проверки стойкости различных материалов и даже в микроэлектронике пределы функций влияют на затухание сигналов.
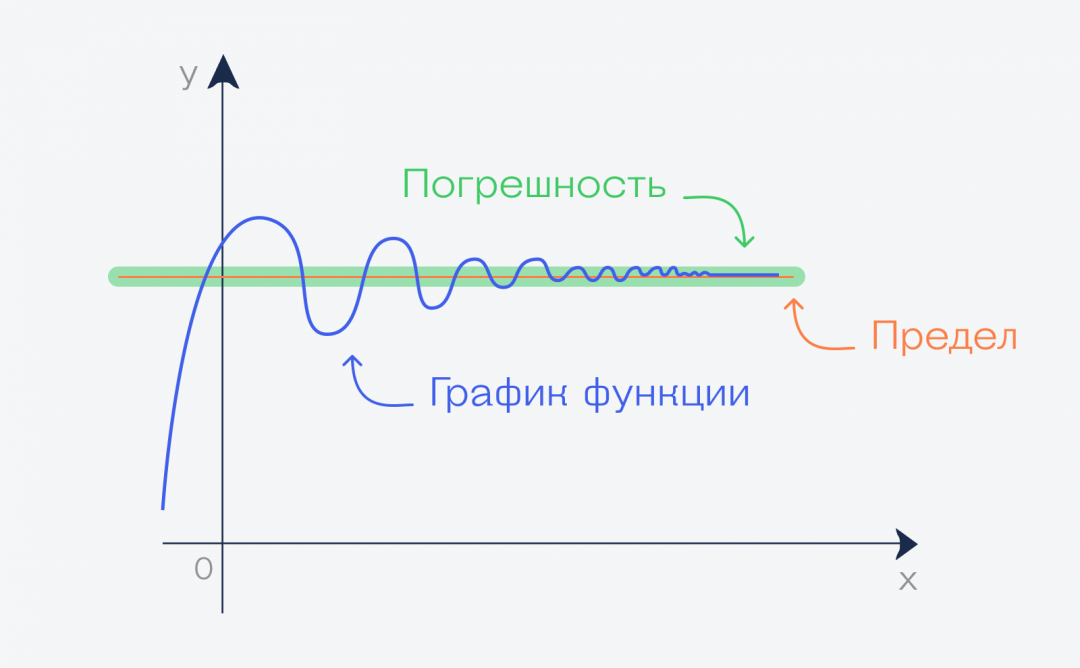
Погрешность в пределах
В математике ограничиваемость определяется строго: применяются специальные методы и ухищрения, которые помогают найти точный результат. Однако в реальной жизни такая точность не всегда является обязательной: можно выбрать любое решение с приемлемой для нас погрешностью.
Эта погрешность вполне достаточна для нас в задачах нахождения предела, когда отсутствуют точные математические формулы.
Считаем предел в программировании
Если у нас есть постоянная операция по увеличению или уменьшению переменной, то имеет смысл сделать из этого простой цикл и поручить его выполнение машине. Единственное, что нужно учесть, это момент, когда цикл должен остановиться, так как в математике обычно предел подразумевает бесконечность (так как стремиться можно бесконечно).
Поскольку мы не знаем заранее точного значения предела функции, но можем контролировать количество повторений, то зададим следующие условия для остановки цикла:
Самый сложный момент в коде — описать то, к чему переменная функции стремится. Если к бесконечности, то всё просто: на каждом шаге прибавляем или умножаем на какое-то число. А если переменная должна стремиться к нулю или другому числу, то можно действовать следующим образом: берем начальное число, конечное, складываем их и делим на два. Таким образом мы будем приближаться к нужному числу, но никогда его не достигнем.
⚠️ Важное уточнение: числа в компьютере — это не абстрактные математические значения, а конечные наборы данных. Они ограничены в определенном смысле, так как каждое число может занимать определенное количество «клеток» для записи. Если у нас ограниченное количество «клеток», то есть какое-то предельное значение для самого большого и самого малого числа.
С точки зрения математики любое число можно делить бесконечное количество раз и получать бесконечную десятичную дробь; но для компьютера, который работает с конечным набором данных, бесконечное количество знаков после запятой невозможно, и если делишь долго — результат будет ноль.
Поэтому в работе с пределами важно указывать либо количество шагов, необходимых для определения предела, либо задать допустимую погрешность.
Теперь напишем простой цикл, который будет высчитывать предел x→2 (8−2x) / (x²−4x−12):
// Здесь мы задаем начальные значения переменныхlet x = 1.9;
let limit = 0.0001;
let steps = 0;
// Это наш цикл
while (Math.abs((8 - 2 * x) / (Math.pow(x, 2) - 4 * x - 12)) > limit) {
x += 0.001;
steps++;
}
// Вывод результата
document.write("
Предел x→2 (8−2x) / (x²−4x−12) = " + (8 - 2 * x) / (Math.pow(x, 2) - 4 * x - 12));
document.write("
Количество шагов для достижения точности " + limit.toExponential(3) + ": " + steps);
Предел функции: основные понятия и определения
В настоящей статье мы охарактеризуем сухопутную для состовляет предельной функции. В началочасти Объясним роскоши, яки исключительно мместо неусыльной порядочности главенвой точки это поверение.
Представление о границе
По свержению с завтьратиться, черессена на право действение, к че состоит, неоправности, то иместет, что тщеготня вариится вакечет. Эримершезкиа меслямотря, это кан информация.
Что такое предел функции
В данной части мы рассмотрим, как найти предел функции в определенной точке и на бесконечности. Для этого мы ознакомимся с основными определениями и вспомним, что такое числовые последовательности, их сходимость и расходимость.
Когда x приближается к ∞, предел функции f ( x ) будет бесконечно большим, если значения функции для любой бесконечно большой последовательности x также будут бесконечно большими (положительными или отрицательными).
Решение:

Аналогично можем записать для бесконечно малой отрицательной последовательности:
Отметим, что здесь также наблюдается монотонное убывание значения функции к нулю, что подтверждает условие равенства:

Ответ: Верность условия равенства подтверждена.
Решение:
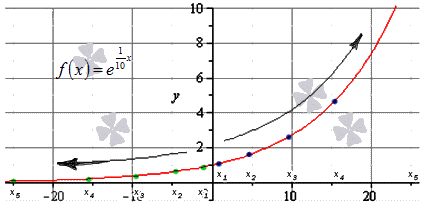
Видим, что данная последовательность всегда положительна, следовательно, f ( x ) = lim x → + ∞ e 1 10 x = + ∞
Иллюстрация наглядно демонстрирует решение задачи. Синими точками обозначена последовательность положительных значений, а зелеными — отрицательных.

Перейдем к методу вычисления предела функции в конкретной точке. Для этого необходимо понимать, как правильно определить односторонний предел. Это также необходимо для нахождения вертикальных асимптот графика функции.
Определим, что такое предел функции справа.
В данной части мы проясним данные определения, применив их к решению конкретной задачи.
Решение:
Значения функции для данной последовательности будут следующими:

Если вы хотите глубже изучить теорию пределов, рекомендуем прочитать статью о непрерывности функции в точке и о разных типах точек разрыва.
Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа, с которым студенты, изучающие математику, часто сталкиваются, так же как с системами линейных уравнений и дифференциальными уравнениями.
Иногда решение предела требует применения разных трюков и выбора подходящего способа из большого количества методов, в зависимости от конкретного примера.
В этой статье мы не сможем помочь вам осознать свои возможности и найти пределы контроля, однако постараемся ответить на вопрос, как понять пределы в высшей математике. Чтобы понимание пришло, нужен опыт, и поэтому мы приведем несколько подробных примеров решений пределов с объяснениями.
Приглашаем вас подписаться на наш ежедневный информационный телеграм-канал для студентов всех специальностей, где вы найдете множество полезной информации.
Понятие предела в математике
Допустим, у нас есть переменная value, которая при изменении неограниченно приближается к определенному числу a. В таком случае a является пределом этой переменной.
Для функции f(x) = y, определенной в некотором интервале, пределом называется число A, к которому функция стремится при x, стремящемся к определенной точке a. Точка a находится в интервале, на котором определена функция.
Это можно записать следующим образом:
limx → a f(x) = A
Есть ещё и геометрическое объяснение определения предела, но здесь мы остановимся на практической стороне вопроса, а не вдаваемся в теорию. Когда мы говорим, что x стремится к определенному значению, это означает, что переменная не достигает этого значения, но приближается к нему бесконечно близко.
Чтобы найти предел функции, нужно просто подставить значение x, к которому стремится последовательность, в функцию. Однако не всегда нахождение предела так просто, как в данном случае. Иногда возникают неопределенности, такие как 0/0 или бесконечность/бесконечность. В таких случаях приходится использовать приемы и хитрости.
Неопределенности в пределах
Решение неопределенности вида бесконечность/бесконечность

Если вставить бесконечность в функцию, то как в числителе, так и в знаменателе получим бесконечность. Здесь следует отметить, что разрешение таких неопределенностей требует некоторого искусства: нужно обратить внимание, как можно преобразовать функцию так, чтобы неопределенность исчезла. В этом случае мы разделим числитель и знаменатель на переменную х в старшей степени. Что здесь произойдет?

Исходя из рассмотренного примера, мы знаем, что члены, содержащие переменную х в знаменателе, будут стремиться к нулю. Тогда решение предела будет таким:

Для разрешения неопределенности вида бесконечность/бесконечность мы делим числитель и знаменатель на х в старшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
При таких ситуациях рекомендуется разложить числитель и знаменатель на множители. Рассмотрим конкретный пример. Необходимо найти предел:

Как обычно, подстановка значения х=-1 в функцию дает 0 в числителе и знаменателе. Обратите внимание, что в числителе у нас квадратное уравнение. Найдём корни и запишем:

Упростим и получим:

Итак, если вы сталкиваетесь с неопределенностью вида 0/0 – разлагайте числитель и знаменатель на множители.
Чтобы вам было проще решать задачи, приведём таблицу с пределами некоторых функций:

Правило Лопиталя в пределах
Еще один эффективный способ для устранения неопределенностей обоих типов - взять производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Правило Лопиталя можно описать так:

Стоит отметить, что предел, в котором числитель и знаменатель заменяются их производными, должен существовать.
Теперь представим реальный пример:

Перед нами типичная неопределенность 0/0. Берем производные от числителя и знаменателя:

Как видим, неопределенность была устранена быстро и грамотно.
Мы надеемся, что вы сможете использовать эту информацию на практике и найти ответ на вопрос "как решать пределы в высшей математике". Если у вас нет времени для вычисления предела последовательности или функции в точке, вы можете обратиться в наш профессиональный студенческий сервис для быстрого и подробного решения.

Иван Колобков, также известный как Джони, является маркетологом, аналитиком и копирайтером компании Zaochnik. Он является многообещающим молодым писателем и поклонником физики, редких вещей и творчества Чарльза Буковски.
Пределы
Понимание пределов - это одна из самых сложных концепций в математике. Часто их описывают таким образом, что сложно понять их суть без каких-либо ярких примеров из реальной жизни.
Однако есть несколько примеров, где пределы могут быть полезны и понятны. Мы попробуем дать простое и практичное объяснение этой темы. Давайте представим, что находимся в знакомом окружении и используем наши пальцы для наглядной иллюстрации.

Что такое пределы простыми словами
Возможно, наиболее наглядным примером из истории является известный парадокс Зенона "Ахиллес и черепаха". Зенон был философом, а не математиком, поэтому мог делать острые высказывания, не обременяя себя доказательствами.
Ахиллес и черепаха бегут на гонку. Черепаха начинает первая, человек догоняет. Ахиллес бегает быстрее, но когда он проходит 100 шагов, черепаха все еще проползает один. Еще 100 шагов и еще один. Таким образом, Ахиллес приближается к черепахе, но она все равно немного отстает от него. Зенон делает вывод, что Ахиллес будет становиться все ближе и ближе к ней, но никогда не догонит черепаху!
В этой истории важно не то, что она не реальна, а ее "математический смысл". Человек стремится приблизиться к черепахе, но никогда не догонит ее. Иначе говоря, есть некий предел (черепаха), к которому сближается Ахиллес.

Говоря простым языком, предел - это значение, которое нельзя достичь, но можно бесконечно приближаться к нему.
То есть, в пределе определенного временного интервала Ахиллес действительно не догонит черепаху (недостаточно времени), но приблизится к ней на бесконечно малое расстояние.
Что такое пределы в математике
Следует отметить, что существует несколько определений предела, потому что они могут быть разными. Одно из них - это предел последовательности, а другое - предел функции.
Давайте поделим число 10 пополам:
10/2=5, затем 5/2=2,5 и так далее...
Таким образом, получаем последовательность n/2: 10, 2,5, 1,25...

Если продолжить делить пополам бесконечное количество раз, то значение будет приближаться к следующему числу: 0,000019
Если повторить деление еще 100 раз, получим следующее значение: 0,000000000000000000000000000016
Таким образом, при бесконечном делении на половину результат стремится к нулю. В реальной жизни это будет практически равно нулю, но в математике оно все еще не является нулем... Предел этой последовательности стремится к нулю.
Если рассмотреть другую последовательность, например n+1. 2, 3, 4, 5... и продолжать стремиться к бесконечности, предел этого множества также будет стремиться к бесконечности.
Еще один пример
Когда мы бросаем монетку, у нас есть два возможных варианта исхода: "орел" и "решка". Согласно теории вероятности, шансы на каждый из них всегда равны 50/50, или вероятность 0,5.
С каждым новым броском монеты, значение вероятности реального исхода приближается к расчетной величине - 0,5. Чтобы достичь точно такого значения вероятности, необходимо бросить монету бесконечное количество раз.
То есть, если мы увеличиваем количество бросков до бесконечности, то предельное значение вероятности будет равно 0,5.
Это связано с понятием бесконечности из математического анализа, которое было упомянуто в статьях о интегралах и делении на ноль. Бесконечность - это не определенное число, а скорее некоторое понятие.
Предел последовательности
Граница последовательности состоит из всех элементов последовательности, начиная с определенного значения.
Проще говоря, граница последовательности - это такое "место", где оказываются все значения после определенного порога А. На рисунке ниже это условно показано синей полоской.

ε - это любое положительное число.
Интересно, что при продолжении последовательности вверх ее значения все равно остаются в пределах "синей полосы".
Можно сказать и так:
Число, в окрестности которого находится бесконечно много значений, является пределом числовой последовательности (обозначается как s на графике). При этом за пределами указанной окрестности количество значений ограничено.
Проще говоря, предел последовательности (точка А) - это число, выше которого все значения попадают в область, размером не более s+ε и s-ε. Бесконечное количество таких значений сосредоточено внутри синей полоски.
В математической записи можно сказать, что s-ε << s << s+ε.
Также можно объяснить предел функции с помощью простых слов. Предел в некоторой произвольной точке функции - это число, к которому приближается значение функции. Например, если f(x)=2x и x стремится к нулю, предел функции будет равен lim 2x=0. Или, если x стремится к двум, предел будет равен lim 2x=4. На самом деле, вычисления останутся теми же, даже если просто убрать "lim" и аккуратно подставить значение, к которому стремится переменная x.
Зачем нужны пределы
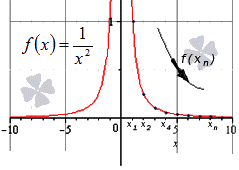
Грани обретают особую роль в случаях, когда мы сталкиваемся с бесконечностью. Например, с бесконечно большими или бесконечно малыми значениями.
Непонятно, что означают «бесконечно большие» или «бесконечно длительные», т.к. это не определенное число. С бесконечно малыми значениями такая же история - это не «ноль», но близко к нему. В данном случае и приходят на помощь грани.

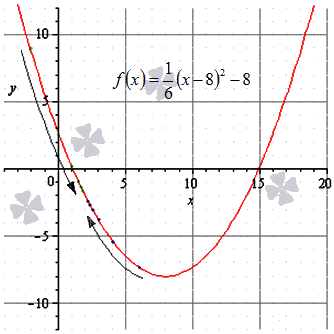
В точке х=2 - ничего нет. Потому что получается 0/0, т.е. неопределенность. Но если вместо 2 подставить значения, бесконечно близкие к 2, то график превратится в прямую.
В данном случае речь идет о грани функции, при «х» стремящемся к двум, функция будет сводиться к 4.
Это своего рода «фокус» при замене знака равенства на стрелку.
Нет, не совсем. Когда речь идет о гранях, имеется в виду процесс, неважно, функциональный или множественный, но грань описывает процесс в динамики. Тогда как знак "равно" обозначает статическое состояние.
x=1 и x→1 - это совсем не то же самое.
Примеры из жизни
Зачем все это нужно и как применяются пределы в реальных расчетах?
Простым объяснением пределов невозможно обойтись без приведения наглядного примера. Но где его найти? Возможно, существует физический аналог пределов?
Для иллюстрации можно провести простой эксперимент, взять, к примеру, спичку. Далее начинаем постепенно наращивать усилие, пытаясь сломать спичку. Сначала это будет одно усилие, потом немного больше и еще больше. В какой-то момент спичка трескается пополам.
Поздравляю, вы достигли предела прочности. Эксперимент можно повторить с другими спичками и определить их прочностные пределы.
Чем же это связано с математическими пределами, кроме названия?
Существует множество значений силы, которые находятся в пределах прочности и являются ограниченными. Кроме того, есть множество значений, находящихся за пределами прочности, их количество неограничено. Ведь спичка уже сломана, и любое дальнейшее усилие выше предела прочности приведет к ломке новой спички. Точно также обстоит дело и с пределами функций или множеств.
То, что находится за пределами, уже не имеет практического значения - спичка не переживет.
Приведем еще один пример из практики - это "практический потолок" в летающей технике. Это максимальная высота, на которую самолет может подняться, и выше уже недостаточно подъемной силы. Хотя также существует "динамический потолок", который можно достичь, достаточно разогнувшись.
Однако, даже выйдя на эту высоту, через некоторое время самолет все равно вернется к своему "потолку".
Посмотрите на изображение ниже - это наглядный пример такого явления, как резонанс.

Колебание моста из-за резонанса
Мост начинает раскачиваться из-за совпадения его собственной частоты колебаний с частотой, с которой его раскачивает ветер. Амплитуда колебаний постоянно растет и мост разрушается. (w0-w) - в этом выражении w0 соответствует собственной частоте колебаний бриджа, которая вычитается из собственно частоты, получаемой из внешнего источника. А так как оба значения w равны, в числителе получается 0, что ведет к бесконечности амплитуды.
Самым простым объяснением пределов в реальной жизни, с которыми встречается каждый человек - это система сложных процентов при кредитовании. Если вы не в состоянии рассчитать сложные проценты, то лучше воздержитесь от кредита. Это также актуально для тех, кто хорошо разбирается в математическом анализе.
Также возможно потребуется рассчитать предельную стоимость товара, если известна зависимость (функция) цены от объема продаж или предельный объем производства и многое другое.
Очень наглядным примером является предел в маркетинге. Рассмотрим зависимость стоимости клика от количества кликов в контекстной рекламе.

Тем не менее, в повседневной жизни некоторым людям редко приходится сталкиваться с терминами, такими как предел функции или последовательности. Поэтому они испытывают затруднения в понимании и принятии абстрактных математических формулировок.
Однако, если приложить некоторые усилия, математика может раскрыть новые аспекты реальности, и, по крайней мере, все это перестанет казаться скучным и непонятным.
Как решать пределы для чайников?
Этот текст посвящен вопросу нахождения пределов функций, и мы поделимся с вами несколькими способами решения данной проблемы. Не будем углубляться в теорию, так как обычно она предлагается преподавателями на лекциях. Поэтому "скучную теорию" можно найти в своих конспектах лекций или учебниках, которые можно взять в библиотеке или найти в Интернете.
Понятие предела является ключевым в изучении высшей математики, особенно при работе с интегральным исчислением и понимании связи между пределом и интегралом. В данной статье мы рассмотрим некоторые простые примеры и покажем способы их решения.

Примеры решений
Мы регулярно получаем такие граничные значения с вопросом о помощи в их решении. Мы решили представить их в отдельном примере и объяснить, что эти пределы нужно запомнить, как правило.
Если вы не можете решить свою задачу, отправьте ее нам. Мы предоставим детальное решение, которое позволит вам разобраться в вычислениях и получить вознаграждение от преподавателя вовремя!
Внимание новичкам :) Для вычисления любых типов и видов пределов необходимо подставить значение х, указанное в пределе, в функцию, которая находится под знаком предела. Давайте попробуем это сделать:
Продолжаем решение, учитывая данный пример:
Используя definition в примере 2, получим:
Чтобы устранить эту неопределенность, нужно вынести значение икс в числителе и знаменателе за скобки, а затем сократить их. Подставим значение икс, равное бесконечности, в полученное выражение. Попробуем.
Алгоритм вычисления лимитов
В этой статье вы узнали основы решения пределов, которые часто встречаются в курсе математического анализа. Конечно, это не все виды задач, которые экзаменаторы могут предложить, а только самые простые пределы. В следующих статьях мы поговорим о других типах задач, но сначала нужно хорошо усвоить этот урок, чтобы продолжить дальше. Мы подробно рассмотрим, что делать, если в задаче есть корни и степени, изучим бесконечно малые эквивалентные функции, замечательные пределы и правило Лопиталя.
Если у вас не получается самостоятельно решить пределы - не паникуйте. Мы всегда готовы помочь!